Magma (mathematica)
Apparentia
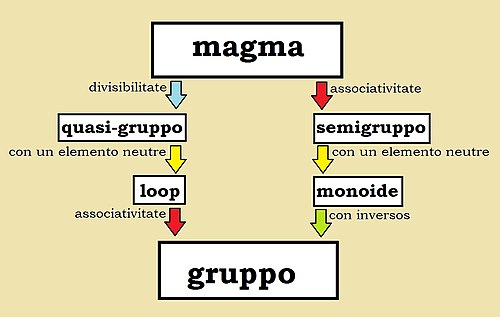
In mathematica un magma[1] es un structura algebric que consiste de un non vacue insimul e un operation binari tal que pro omne existe . Si le operation es commutative, le magma se nomina commutative o abelian. Si le operation es associative, le magma se nomina associative o un semigruppo. Si vale le divisibilitate, le magma es un quasigruppo.
Un apte possibilitate de presentar un magma es le tabellas de Cayley.
Gruppoide
[modificar | modificar fonte]Un ancian nomine a evitar es gruppoide que collide con le homonyme gruppoide del theoria de categorias.
Proprietates
[modificar | modificar fonte]- Si le operation del magma es partial, le magma se nomina partial o un pseudomagma.
- Magma medial
- Magma unipotente
- Magma zeropotente





